Tour de micrograd
Step by step build of a minimal neural network.
In a separate post, I did a selective pass over the development of artificial neural networks to highlight baked in design choices. That exploration was prompted by wanting to know the why behind implementation details of one of the fundamental building blocks of large language models: a basic neural net model with an autograd engine for updating model parameters during training (i.e., learning!).
As a warm up to a Rust implementation of Andrej Karpathy’s tiny neural net, micrograd, I’d written my own Python version. We’ll use that here to explore coding up a bare-bones neural network from scratch.
Despite its micro sizing, micrograd has all the essentials: nodes, edges, weights, biases, activation functions, layers (input, hidden, output), loss metric, backpropagation, and stochastic gradient descent. All built into a multilayer perceptron (MLP) model.
The compact codebase has core functionality organized into just 2 files of less than 200 lines each. Snippets are referenced below, and the full code repository is on GitHub as msyvr/micrograd-python under an Apache 2.0 license.
Network design
Let’s translate those design choices into a rough plan for the key players in our network, namely: neurons, layers, MLP, autograd (backpropagation + gradient descent).
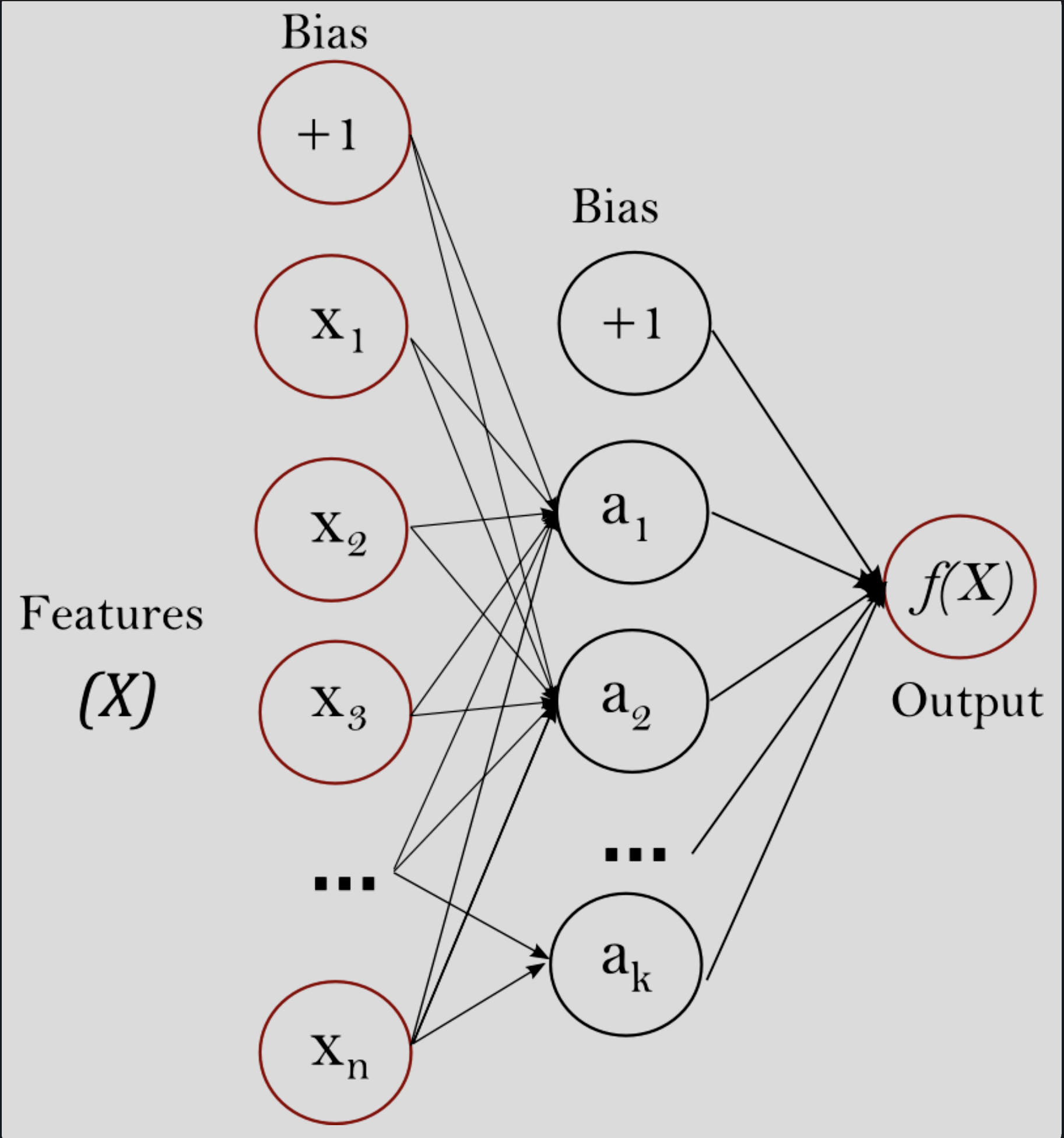
A reference schematic for the MLP network structure might come in handy.
Figure 1. Basic MLP schematic (Scikit Learn).
Essential specs
Here’s a list of the core neural network design choices derived in an earlier post, Designing neural networks: zero to micrograd:
-
Use a multilayer perceptron network architecture.
- Corollary requirement: At least one hidden layer.
- Corollary requirement: Include nonlinear component(s) in the forward pass.
-
Use nonlinear activation functions that mimic neuronal signal propagation.
-
Use feedback to update weights and biases to learn between training passes.
-
Use backpropagation and gradient descent as the learning algorithm.
- Corollary: Use differentiable activation functions.
-
Use mean squared error as the loss metric.
Building on the above, we’ll organize our code around the following:
| Item | Details |
|---|---|
| Neuron | take $N_{in} = N{_{previous\_layer}}$ inputs; linearly combine inputs using scalar weight parameters; add scalar bias; apply a nonlinear activation; return neuron output |
| Layer | set up $N_{paths} = N_{in} * N_{out}$ paths through the layer; process layer-neurons independently; return neuron outputs |
| Network | build ordered layers; set the loss metric; manage neuron parameter updates |
| Autograd | build the topological map; manage neuron state (Value class); implement arithmetic functions and gradients for Value; implement autograd |
| Training | set $N_{epoch}$; set $step\_size$; set $tolerance$; execute training iteration loop |
Code organization
The project file structure (see the Github repo) has core architecture and functionality distributed across three files:
nn.py: Define the neural network’s structural components and implement functionality for each.
autograd.py: Define the update function. Set out how to backpropagate the learning signal to nodes.
train.py: Configure a training run. Define network structure; choose activation and reward/loss functions; declare number of epochs, step size, and tolerance/loss objective.
Component details
nn.py: Build nodes
Initializing the neuron (__init__) sets the number of neuron inputs and assigns each input a random weight. The neuron’s bias is also set randomly.
Random initialization is how we avoid introducing bias at this stage. During training, the network will identify parameters that optimize network performance.
The activation function passed to the initialization function is assigned to the neuron.
Processing the neuron (__call__) has two stages: linear superposition, with coefficients mapped to neuron parameters w and b, followed by activation. Two standard activation functions are implemented: $ReLU$ and $tanh$. You may notice that $ReLU$ isn’t differentiable at 0; in practice, 0 is simply handled explicitly.
A function for accessing a neuron’s parameters is provisioned.
class Neuron:
def __init__(self, nin, activation):
self.w = [Value(random.uniform(-1, 1)) for _ in range(nin)]
self.b = Value(random.uniform(-1, 1))
self.activation = activation
def __call__(self, x):
act = sum((wi*xi for wi, xi in zip(self.w, x)), self.b)
out = act.relu() if self.activation == 'relu' else act.tanh()
return out
def parameters(self):
return self.w + [self.b]
You might be wondering about the Value class. Looking ahead, we’ll need to pass neuron parameters along with other relevant data to implement gradient descent during training. Value will support that; we’ll revisit it later.
nn.py: Build a layer
Initializing the layer (__init__) creates nout neurons, each with nin inputs to represent all the forward-pass paths through the current layer. The layer’s activation function is also set.
Processing the layer (__call__) involves processing the current layer’s neurons and returning the results.
A function for returning the layer’s neuron parameters is provisioned.
class Layer:
def __init__(self, nin, nout, activation):
self.neurons = [Neuron(nin, activation) for _ in range(nout)]
def __call__(self, x):
outs = [n(x) for n in self.neurons]
return outs[0] if len(outs) == 1 else outs
def parameters(self):
return [p for neuron in self.neurons for p in neuron.parameters()]
nn.py: Build a network
Next, the layers are composed into an ordered structure, emulating an MLP network.
Initializing the MLP network (__init__) defines its layers. A layer ‘size’ represents the sum total of its neurons’ inputs and outputs; collectively, the layer sizes establish the indexing to access any given layer within the network structure. Each layer is also assigned an activation function.
Processing the MLP network (__call__) involves processing each layer and returning the final output of the network.
A function for returning the network’s neuron parameters is provisioned.
With loss evaluated at the network level, gradient descent is managed from this abstraction layer. Gradient reset is provisioned with zero_grad. Neuron parameter updates are provisioned per the neuron’s grad parameter scaled by the global step. (See note on step size in the train.py section.)
class MLP:
def __init__(self, nin, nouts, activation, step):
sz_io = [nin] + nouts
self.layers = [Layer(sz_io[i], sz_io[i+1], activation) for i in range(len(nouts))]
self.step = step
def __call__(self, x):
for layer in self.layers:
x = layer(x)
return x
def parameters(self):
return [p for layer in self.layers for p in layer.parameters()]
def zero_grad(self):
for p in self.parameters():
p.grad = 0.
def update_parameters(self):
for p in self.parameters():
p.data += self.step * -p.grad
autograd.py: Backpropagation
Take a look at the MLP schematic and note the many distinct forward pathways through the network. To propagate the loss back through the network, we’ll need to reverse each forward path.
The backward function creates the topological map recursively.
def backward(self):
topo = []
visited = set()
def build_topo(v):
if v not in visited:
visited.add(v)
for child in v._prev:
build_topo(child)
topo.append(v)
build_topo(self)
self.grad = 1.0
for node in reversed(topo):
node._backward()
autograd.py: Gradient descent
To implement gradient descent, nodes need a data structure to store not only their weight and bias parameters, but also local gradient, position in the topological map, and origin operation. For this, the Value class is defined. Functions defined for this class cover everything needed for forward passes and for implementing gradient descent.
class Value:
def __init__(self, data, _children=(), _op='', label=''):
self.data = data
self.grad = 0.0
self._backward = lambda: None
self._prev = set(_children)
self._op = _op
self.label = label
Beyond initialization, there’s a fair bit of functionality to implement for Value. Most of it is straightforward, setting up arithmetic functions and their associated gradients. Details are in the full code repository on GitHub.
An example gradient implementation of $tanh$, one of the activation function options:
def tanh(self):
x = self.data
t = (math.exp(2*x) - 1)/(math.exp(2*x) + 1)
out = Value(t, (self, ), 'tanh')
def _backward():
self.grad += (1 - t**2) * out.grad
out._backward = _backward
return out
train.py: Run it!
Essentially, a script to train the model. It runs nested loops over $N_{evals}$ and $N_{epochs}$. Epochs represent model training, and each iteration contributes to the overall loop. Evals represent model outputs for distinct training runs, so each iteration runs independently and we can get a distribution for evaluating model performance.
Training parameters:
Loss function: The choice of loss metric depends on the model objectives. For micrograd, MSE is fine.
Step size: Sets a limit on the effective resolution of hitting the target. In practice, a compromise is made between too small (updates too slowly) and too large (overshoot the target).
Number of epochs: Sufficient (varied) samples are required to get a good distribution of capabilities and avoid overfitting.
Tolerance: Sets a target for satisfactory performance: if achieved, training will stop even if the maximum number of epochs hasn’t been reached.
Number of evals: Repeat training to evaluate the model’s performance statistics.